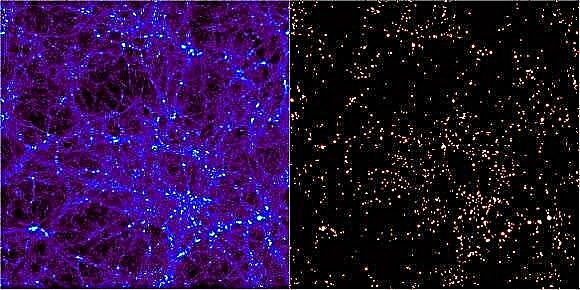
ब्रह्मांड के ΛCDM मॉडल की सफलताओं में से एक यह है कि मॉडल के लिए अंतरिक्ष पत्रिका में जो हम देखते हैं, उसी तरह तराजू और वितरण के साथ संरचनाएं बनाते हैं। जबकि कंप्यूटर सिमुलेशन एक बॉक्स में संख्यात्मक ब्रह्मांडों को फिर से बना सकते हैं, इन गणितीय अनुमानों की व्याख्या करना अपने आप में एक चुनौती है। सिम्युलेटेड स्पेस के घटकों की पहचान करने के लिए, खगोलविदों को संरचना की खोज के लिए उपकरण विकसित करना पड़ा है। परिणाम 1974 के बाद से लगभग 30 स्वतंत्र कंप्यूटर प्रोग्राम रहे हैं। प्रत्येक क्षेत्र में डार्क संरचना के रूप में खोजने के लिए ब्रह्मांड में संरचना बनाने का वादा करता है। इन एल्गोरिदम का परीक्षण करने के लिए, 2010 के मई के दौरान मैड्रिड, स्पेन में एक सम्मेलन आयोजित किया गया था जिसका शीर्षक था "हेलो गोइंग एमएडी" जिसमें इन कोडों में से 18 को परीक्षण में यह देखने के लिए रखा गया था कि वे कितनी अच्छी तरह से ढेर हो गए हैं।
ब्रह्मांड के लिए संख्यात्मक सिमुलेशन, जैसे प्रसिद्ध मिलेनियम सिमुलेशन "कणों" से अधिक कुछ भी नहीं के साथ शुरू होता है। जबकि ये ब्रह्माण्ड संबंधी पैमाने पर निस्संदेह छोटे थे, ऐसे कण लाखों या अरबों सौर द्रव्यमान के साथ काले पदार्थ की बूँद का प्रतिनिधित्व करते हैं। जैसे-जैसे समय आगे बढ़ता है, उन्हें एक-दूसरे के साथ निम्नलिखित नियमों के साथ बातचीत करने की अनुमति मिलती है जो भौतिकी की हमारी सबसे अच्छी समझ और इस तरह के मामले की प्रकृति के साथ मेल खाते हैं। यह एक विकसित ब्रह्मांड की ओर जाता है जहाँ से खगोलविदों को जटिल कोड का उपयोग करके अंधेरे पदार्थ के समूह का पता लगाना चाहिए जिसके अंदर आकाशगंगाएँ बनती हैं।
इस तरह के कार्यक्रमों का उपयोग करने वाली मुख्य विधियों में से एक छोटी मात्रा में खोज करना है और फिर इसके चारों ओर एक गोलाकार खोल विकसित करना है जब तक कि घनत्व एक नगण्य कारक से गिर न जाए। अधिकांश तब मात्रा के भीतर के कणों को चुभेंगे, जो गुरुत्वाकर्षण के लिए बाध्य नहीं हैं, यह सुनिश्चित करने के लिए कि डिटेक्शन तंत्र बस एक संक्षिप्त, क्षणिक क्लस्टरिंग पर जब्त नहीं होता है जो समय के साथ गिर जाएगा। अन्य तकनीकों में आस-पास के समान वेग वाले कणों के लिए अन्य चरण रिक्त स्थान खोजना शामिल है (एक संकेत है कि वे बाध्य हो गए हैं)।
तुलना करने के लिए कि प्रत्येक एल्गोरिदम का प्रदर्शन कैसे हुआ, उन्हें दो परीक्षणों के माध्यम से रखा गया। सबसे पहले, जानबूझकर निर्मित डार्क मैटल हैलॉग की एक श्रृंखला को शामिल किया गया। चूंकि कण वितरण जानबूझकर रखा गया था, इसलिए कार्यक्रमों से आउटपुट को हॉल्ट के केंद्र और आकार को सही ढंग से ढूंढना चाहिए। दूसरा परीक्षण एक पूर्ण विकसित ब्रह्मांड सिमुलेशन था। इसमें वास्तविक वितरण का पता नहीं चलेगा, लेकिन सरासर आकार अलग-अलग कार्यक्रमों को एक ही डेटा सेट पर तुलना करने की अनुमति देगा, यह देखने के लिए कि उन्होंने समान स्रोत की व्याख्या कैसे की।
दोनों परीक्षणों में, सभी खोजकर्ताओं ने आम तौर पर अच्छा प्रदर्शन किया। पहले परीक्षण में, अलग-अलग कार्यक्रमों के आधार पर कुछ विसंगतियां थीं कि कैसे अलग-अलग कार्यक्रमों ने हैलोस के स्थान को परिभाषित किया। कुछ ने इसे घनत्व में शिखर के रूप में परिभाषित किया, जबकि अन्य ने इसे द्रव्यमान के केंद्र के रूप में परिभाषित किया। जब सब-हैलोस की खोज करते हैं, तो चरण स्थान दृष्टिकोण का उपयोग करने वाले लोग छोटे संरचनाओं का अधिक मज़बूती से पता लगाने में सक्षम होते हैं, फिर भी हमेशा यह नहीं पता लगा पाए कि वास्तव में कौन से कण गांठ में थे। पूर्ण सिमुलेशन के लिए, सभी एल्गोरिदम असाधारण रूप से अच्छी तरह से सहमत हुए। अनुकरण की प्रकृति के कारण, छोटे पैमानों का अच्छी तरह से प्रतिनिधित्व नहीं किया गया था, इसलिए इन संरचनाओं का पता लगाने के तरीके की समझ सीमित थी।
इन परीक्षणों के संयोजन ने किसी भी अन्य पर एक विशेष एल्गोरिथ्म या विधि का पक्ष नहीं लिया। यह पता चला कि प्रत्येक आम तौर पर एक दूसरे के संबंध में अच्छी तरह से कार्य करता है। स्वतंत्र तरीकों के साथ इतने सारे स्वतंत्र कोड की क्षमता का मतलब है कि निष्कर्ष बेहद मजबूत हैं। ब्रह्मांड के बारे में हमारी समझ विकसित होने के बारे में वे जो ज्ञान देते हैं वह खगोलविदों को ऐसे मॉडलों और सिद्धांतों का परीक्षण करने के लिए अवलोकन योग्य ब्रह्मांड की मौलिक तुलना करने की अनुमति देता है।
इस परीक्षण के परिणामों को एक पेपर में संकलित किया गया है जो रॉयल एस्ट्रोनॉमिकल सोसायटी के मासिक नोटिस के आगामी अंक में प्रकाशन के लिए स्लेट किया गया है।